Ibo Bonilla Oconitrillol
¿Por qué pentágonos y hexágonos aparecen por todo lado en la Naturaleza?
¿Qué inédita relación hay entre los hexágonos y la proporción áurea?
¿Qué inédita relación hay entre pentágonos y hexágonos?
CON FONDO BLANCO: DESCARGAR EN PDF (AQUÍ)
Después de décadas de hacerme esas preguntas, Keylor Navas hace un paradón en un partido de fútbol soccer, besa la bola y gracias al zoom de la tele, caigo en cuenta en que los hexágonos y pentágonos regulares son complementarios perfectos para el teseleado esférico, …claro, jamás nunca en el plano 2D, donde por más de 2.600 años los matemáticos con obsesión han buscado tal relación.
En el plano 2D, el panal de abejas muestra el más eficiente uso del espacio disponible, lo mismo que en el grafeno como expresión de la nanotecnología y la química del carbono.
Teselado hace referencia a una regularidad o patrón de figuras que recubren o pavimentan completamente una superficie plana y que cumple con dos requisitos: que no queden espacios y que no se superpongan las figuras.
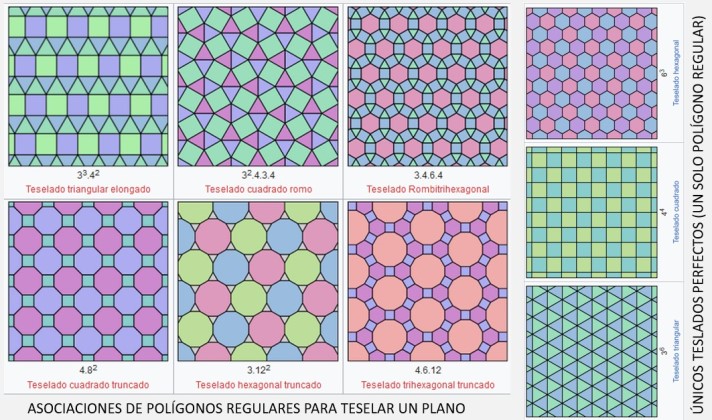
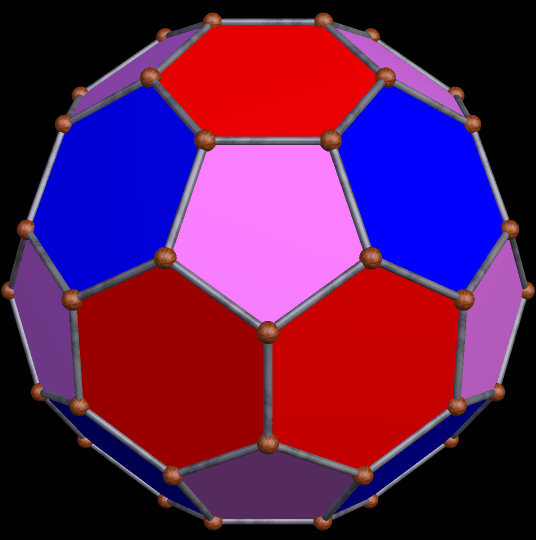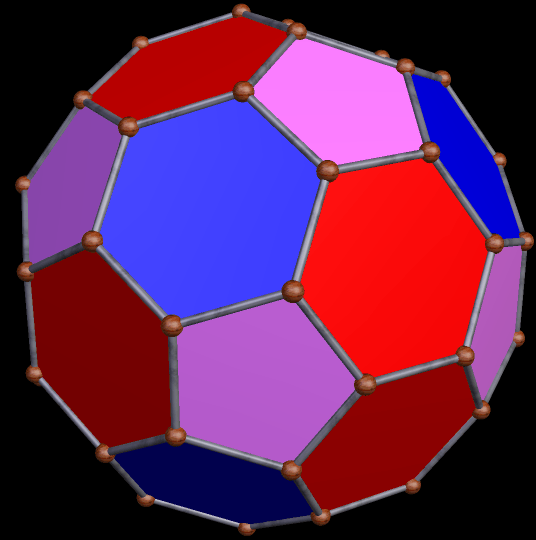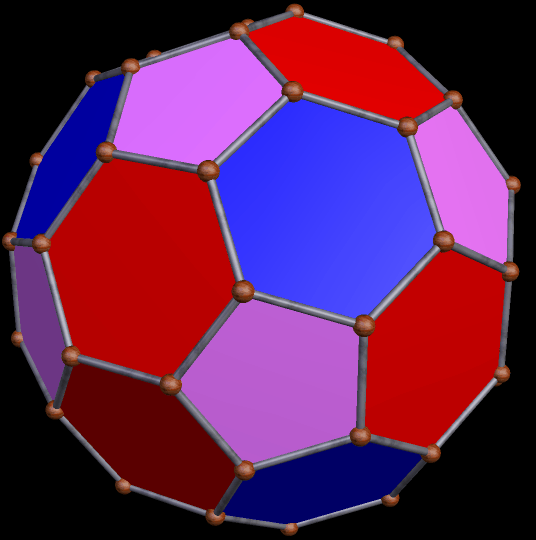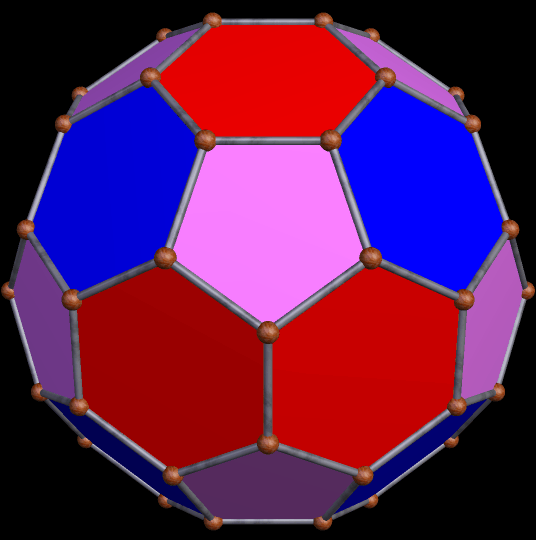
Para las superficies esféricas, se han experimentado muchas opciones y ha sido un atractivo rompecabezas para los matemáticos y artistas aventureros de la complejidad espacial. En su incansable búsqueda de soluciones elegantes, caracterizadas por sencillez, funcionalidad, economía en todas sus facetas y estética, el icosaedro truncado con 12 pentágonos y 20 hexágonos regulares es uno de los favoritos y uno de los teselados más usados en la fabricación de los balones de futbol soccer.
 . .
La intuición me ha dicho que la clave de la respuesta a nuestras preguntas está en la complementariedad de pentágonos y hexágonos, polígonos sucesivos, dan lugar a números poligonales sucesivos y son vecinos colaborativos para el teseleado de superficies esféricas, dada la tendencia natural a la esfericidad de muchos eventos naturales.
Entonces, usando los principios matemáticos clásicos de demostración geométrica,
debemos contestar estas preguntas:
¿Se puede construir un pentágono a partir de un hexágono y viceversa?
¿Se puede demostrar una íntima relación del pentágono y hexágono y la proporción áurea?
¿Está involucrada la Vesica Piscis en estas demostraciones?
Desde ya vamos a decir y demostrar que SÍ, ...y lo haremos a partir de Vesica Piscis.
Por tradición y encanto, usaremos los clásicos procedimientos de regla compás del maestro Euclides de Alejandría, basados en el método deductivo, a partir de la lógica y postulados, lo que garantiza la validez de las conclusiones.
Por seguridad y exactitud lo verificamos con CAD (Diseño Asistido por Computadora) y software de geometría analítica en línea.
Veámoslo:
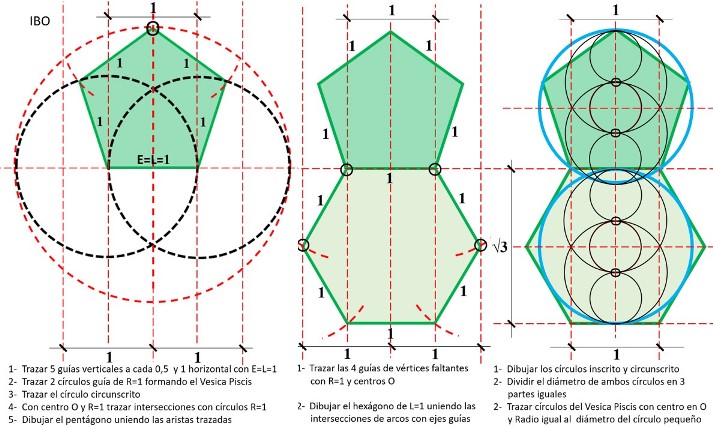
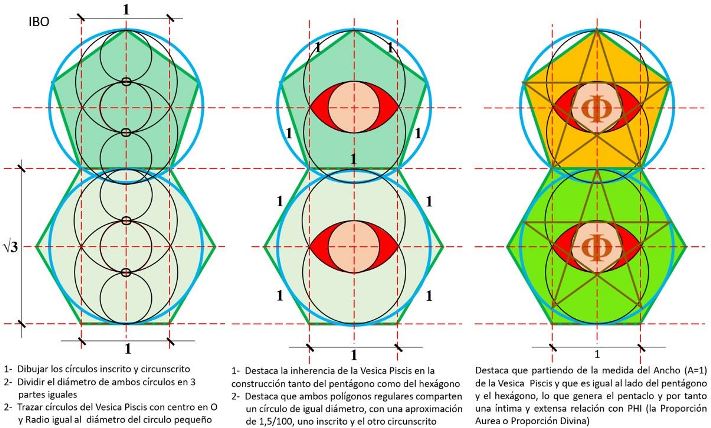
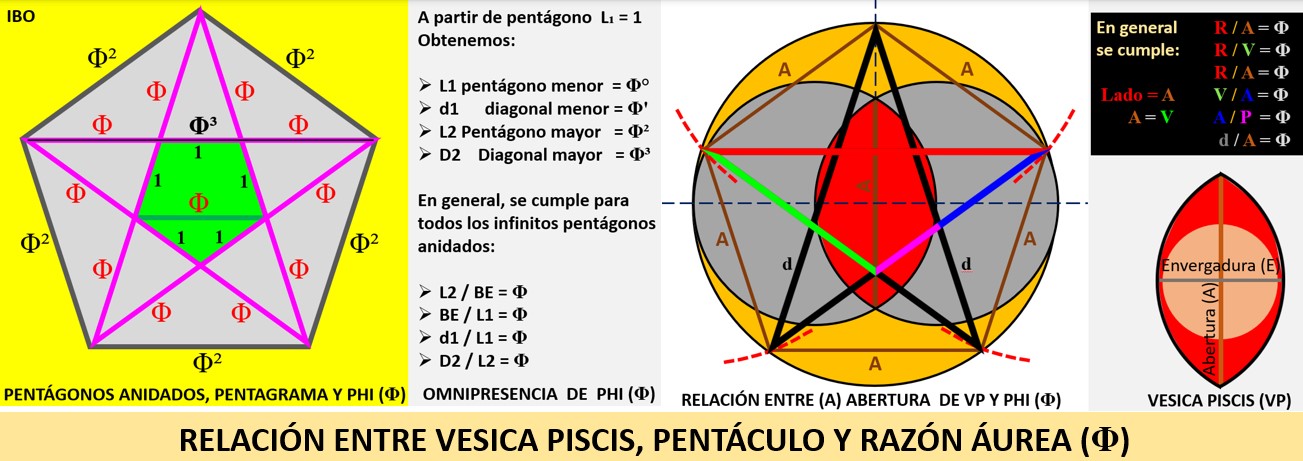
Vesica Piscis, abertura y pentáculo:
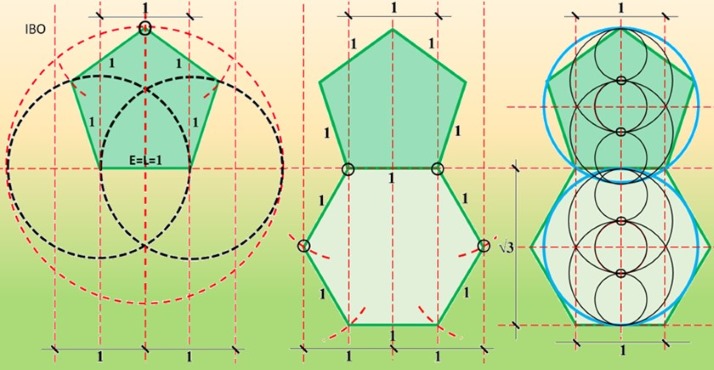
A partir de la Vesica Piscis con Abertura (A=1) se genera automáticamente interesantísimo pentágono unitario L=A=1 (pentágono verde de la siguiente ilustración), que al extender sus lados genera una estrella de 5 puntas (pentáculo pitagórico), que a su vez produce otro pentágono (lila), …y así sucesivamente con pentágonos áureos anidados hasta el infinito en ambas direcciones.
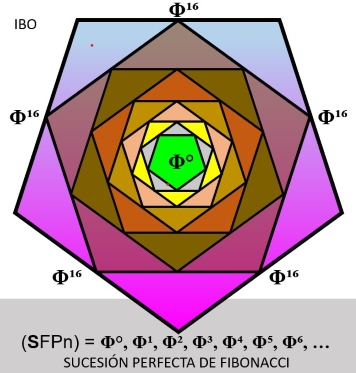
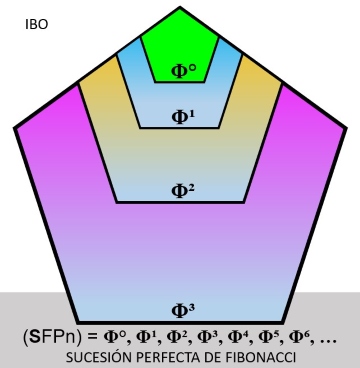
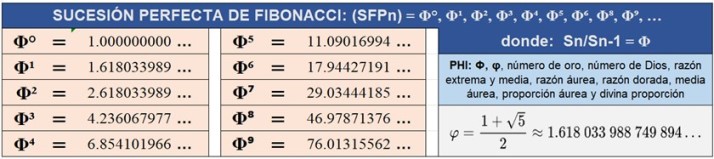
Así se genera la Sucesión de Fibonacci Perfecta, (SFPn) = Φ°, Φ¹, Φ², Φ³, Φ⁴, Φ⁵, …
donde: Sn/Sn-1= Φ (el único caso donde el cociente entre un evento y su antecesor es PHI exacto)
Vesica Piscis, envergadura y pentágono áureo:
A partir de la Envergadura 1 (E=1) de Vesica Piscis y el círculo que la circunscribe, con asombrosa fluidez y elegancia genera un pentágono regular de lado 1 (L=E=1), evidenciando la inherencia de ambos.
Luego y aún más asombroso genera un segundo pentágono, que ni más ni menos el icónico pentágono áureo (todos los lados con valor PHI), que obviamente genera una serie de pentágonos anidados, todos con las mismas proporciones ya que la proporción del lado mayor con el menor es siempre de Φ / 1.
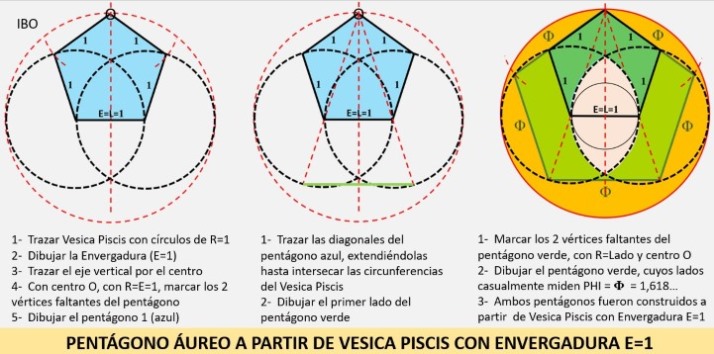
Construcción del hexágono a partir del pentágono e inherencia phi:
Regla sin números y compás como únicos instrumentos, nos siguen encantando como método de demostración geométrico, desde los pre-pitagóricos hasta la fecha, para luego proceder con verificaciones de medición estándar y aritméticas aplicables.
En la actualidad, seguimos la misma práctica, nada más que luego de la intuición o sospecha de alguna hipótesis, se modela con CAD (Diseño Asistido por Computadora) y se verifica con (AP’s) aplicaciones informáticas en línea, para fórmulas reconocidas que incluyen trigonometría avanzada y geometría analítica, aportando rapidez y precisión en ejes, intersecciones, tangentes, particiones, alineaciones, número de decimales, etc.
Así disfrutamos la geometría clásica, un sistema geométrico coherente basados en la lógica axiomática postulada por Euclides, agregando la rapidez y precisión de las herramientas contemporáneas.
Breve historia del balón de fútbol:

Hasta la década de 1930, la pelota con que se jugaba al fútbol era de cuero, con gajos irregulares, neumático independiente con válvula metálica de inflado y cierre con coyunda de cuero (tiento). Representaba un riesgo para los futbolistas, poca estabilidad durante el juego y su vida útil, cambio de peso por humedad y baja funcionalidad para el dominio del balón.
El balón tuvo franjas como los de voleibol durante las décadas de 1950 y 1960.
En la Copa Mundial de 1962, Chile dispuso su pelota oficial, llamada Crack, con forma esférica regular al presentar paneles concentrados, estableciendo el estilo actual. Logró una trayectoria y rebote uniforme por su homogeneidad, así como una notoria mayor velocidad, potencia, alcance y precisión al reducir la fricción, lo que permitió aumentar el ritmo de juego y la magnitud del «chanfle», viabilizando la jugada «gol imposible».
En 1962 la empresa danesa Select Sport, introdujo la estructura del icosaedro truncado. Los productores y federaciones internacionales adoptaron dicho diseño por su funcionalidad, estabilidad y control técnico reglamentario.
En 1963 la compañía alemana de equipamiento deportivo Adidas comenzó a fabricar pelotas y se convirtió en la proveedora de la Copa Mundial desde la edición de 1970, debido a su avanzada tecnología y alta calidad. Revistió el cuero con poliuretano: material sintético flexible e inalterable con el frío y humedad, le da brillo, resistencia a la abrasión, mayor impermeabilidad y mantiene su esfericidad y peso distribuido.
En la edición de 1986 el armazón fue reemplazado por cuero sintético con el balón Azteca. Posteriormente con alta tecnología han intentado balones de una pieza integral, pero hasta la fecha, en la práctica intensa, han generado serias críticas de parte de jugadores y expertos deportivos por sus erráticos comportamientos en su trayectoria y rebotes.
Historia rápida del icosaedro truncado:
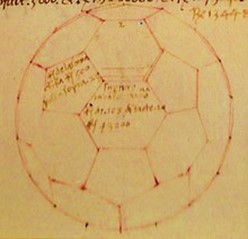
El icosaedro truncado fue conocido por Arquímedes, 287 a.C, quien clasificó los conocidos como 13 sólidos de Arquímedes en un trabajo perdido. Todo lo que se sabe de su trabajo sobre estas formas proviene de Pappus de Alejandría, 290 d.C, quien se limitó a enumerar el número de caras de cada una: 12 pentágonos y 20 hexágonos, en el caso del icosaedro truncado. La primera imagen conocida y descripción completa de un icosaedro truncado proviene de un redescubrimiento de Piero della Francesca,1415, dibujo original adjunto.
Más adelante, Johannes Kepler, 1571, redescubrió la lista completa de los 13 sólidos de Arquímedes, incluido el icosaedro truncado, y los incluyó en su libro de 1609, Harmonices mundi.
Inherencia de la Razón Áurea (PHI, φ) en el icosaedro truncado:
ALas coordenadas cartesianas para los vértices de un icosaedro truncado centrado en el origen son todas permutaciones pares:
(0, ±1, ±3φ)
(±1, ±(2 + φ), ±2φ)
(±φ, ±2, ±(2φ + 1))
donde φ es el número áureo (PHI).
El circunradio es y las aristas tienen longitud 2: .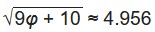
Desde otro ángulo, si la longitud de la arista de un icosaedro truncado es a, el radio de una esfera circunscrita (una que toca el icosaedro truncado en todos los vértices) es:
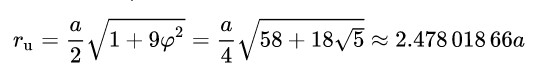
donde φ es el número áureo (PHI).
Este resultado es fácil de obtener utilizando uno de los tres rectángulos áureos ortogonales dibujados en el icosaedro original (antes del corte) como punto de partida para las consideraciones realizadas.
En sus caras planas, la inherencia entre pentágono, hexágono, número áureo (PHI) y Vesica Piscis, se ilustra aquí en forma resumida ahora:
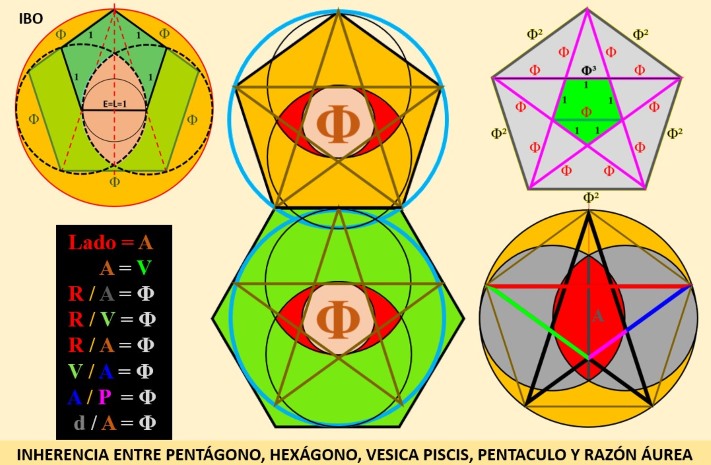
Conclusiones:
El icosaedro truncado (básico en fabricación del balón de fútbol) nos muestra con claridad que los pentágonos y los hexágonos regulares, en la naturaleza y en la matemática, son complementarios, en todas las escalas y dimensiones, y en su génesis lleva una íntima relación con la razón áurea, la Espiral de Fibonacci y Vesica Piscis.
Lo cual nos ratifica que el algoritmo clave de la Creación y evolución del Universo son las Secuencias de Fibonacci, caracterizadas porque cada evento es la suma de los dos anteriores, implicando que el cociente entre un evento cualquiera y su antecedente tiende siempre a la razón áurea (PHI=φ=1,6180…).
Corolario:
La Secuencia Perfecta de Fibonacci, (SFPn) = Φ°, Φ¹, Φ², Φ³, …, es una belleza matemática, pero en la realidad no se da, porque no tiene un mecanismo de auto-correccción, como sí la tiene el ejemplo de los conejos dado por Fibonacci, aunque el cociente entre eventos sucesivos “sólo” tienda a Φ.
Tal como lo predijo Einstein: “cuando las leyes de la matemática se refieren a la realidad, no son exactas, cuando son exactas no se refieren a la realidad”.
En el mundo 3D, nada es matemáticamente exacto ni con simetría absoluta, ni siquiera los “números enteros”, es parte del mecanismo de supervivencia y del sistema de ajuste para desviaciones y traumas.
Por tal motivo, pentágonos, hexágonos y espirales, aparecen desde las partículas elementales, ADN, nanotecnología, hasta escalas galácticas. Tal parece que el único ruido temporal es el producido por acciones antrópicas asociadas a la falta de intuición o ignorancia de las leyes naturales.

BIBLIOGRAFÍA Y REFERENCIAS:
Field, J. V. (1997). «Rediscovering the Archimedean polyhedra: Piero della Francesca, Luca Pacioli, Leonardo da Vinci, Albrecht Dürer, Daniele Barbaro, and Johannes Kepler». Archive for History of Exact Sciences.
McMullen, Peter; Schulte, Egon (2002). «6C. Projective Regular Polytopes». Abstract Regular Polytopes. Cambridge University Press.
Hrant Arakelian. 'The History of the Pentagram', Chapter 6 in 'Mathematics and History of the Golden Section', pp. 207-270, Logos, 2014.
Boyer, Carl Benjamin . «Cap. IV: Jonia y los pitagóricos». Historia de la Matemática (primera edición). Madrid: Alianza Editorial, 1999.
Polyhedra de Realidad Virtual La Enciclopedia de Poliedros
Wolfram Demonstrations Project Mathematica based demonstrations.
Wolfram Language & System Documentation Center
Mathworld. Solid Geometry
El balón de fútbol. Wikipedia
Teseleado regular. Wikipedia
Icosaedro truncado. Wikipedia
Math Calculators. OMNI Calculater
 . .
DESCARGAR EN PDF CON FONDO BLANCO
NOTA: si desea más información sobre el proyecto, puede solicitarla a:
ibobonilla@gmail.com
INICIO / HOME
www.IBOenWEB.com

|

