EL  NÚMERO IMAGINARIO (i)

Realmente complejo pero muy Real  

Por Ibo Bonilla Oconitrillo

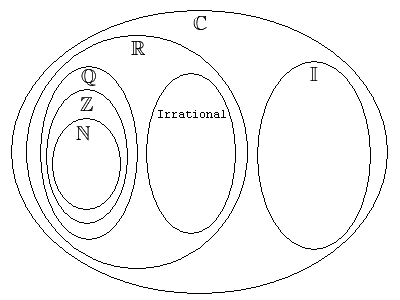
El incomprensible número imaginario, ni siquiera lo clasifican dentro de los Irracionales y menos dentro de los Reales, pero es tan real como un número Irracional, porque I = iⁱ  = i^i = 0,20787958140365...

Es tan real como PI (π = 3,141592…) o PHI (Φ = 1,618033...)

Aquí muestro una demostración fácil y constatable de que el número imaginario se puede expresar como un número irracional cualquiera.

El número imaginario no solo es imprescindible en física y  matemática, sino que es verdaderamente extraño a lo usual y su aplicación es bastante abstracta. Su comprensión ha quemado neuronas de los más notables pensadores.       ... Espero mostrarles que es más cercano de lo que parece.

Un número imaginario es un número cuyo cuadrado es negativo.

El término fue acuñado por René Descartes en el Siglo XVII y se propuso con intenciones  despectivas, aunque es un concepto válido, suponiendo un plano con ejes cartesianos en el que los reales se encuentran sobre el eje horizontal y los imaginarios sobre el eje vertical complejo. Cada número imaginario puede ser escrito como i·r donde r es un número real e ( i ) es la unidad imaginaria, con la propiedad:

En campos de la ingeniería eléctrica y afines, la unidad imaginaria es a menudo escrita como j para evitar la confusión con la intensidad de una corriente eléctrica, tradicionalmente denotada por i.

Cada número complejo puede ser escrito únicamente como una suma de un número real y un número imaginario.

Al número imaginario i se le denomina también constante imaginaria.

Estos números extienden el conjunto de los números reales  al conjunto de los números complejos.

Tiene especial utilidad en electromagnetismo, ondas radiactivas, trayectorias espaciales e indispensables para múltiples problemas matemáticos.

Para agregarle mitología además de llamarlo número imaginario, se le hizo pertenecer al conjunto de los números “complejos”. Lo fantástico que les puedo mostrar es que si bien no cocemos el valor real de i, sí sabemos que i elevada a la potencia i es un número irracional conocido:

  ............................................ UNA SENCILLA DEMOSTRACIÓN

Su demostración puede verla a continuación:

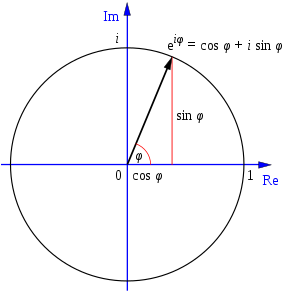
Partiendo de la Fórmula de EULER (1748):

Cos x  + i· sen x = e^ix                (1) (que en geometría circular es muy comprensible)

Sustituyendo  x = π / 2    →     (cos π/2 = 0) y (sen π/2 = 1)

cos π/2 + i· sen π/2 = e^i·π/2  →

     0   +    i ·   ( 1 )    = e^i·π/2  →

    i      = e^i·π/2     (2)

Y elevamos ambos lados a la potencia (i)

Tenemos que:              iⁱ  = e^i·i·π/2  →

                                               iⁱ  = e^-π/2    →

                                               iⁱ  = 1 / e^π/2        →

                                               ^{o bien:}

                                               iⁱ  = √¯e^-π →

                                                iⁱ  = √¯1/e^π       →

donde:

e =  2,71828182845904 ...

π = 3,14159265358979 ...

e^π/2  = 4,810477381 ...

1 / e^π/2  = 0,20787958140365...

!!!!!!! ... Zambomba,... Cáspita, ... Recórcholis, ... Rayos ... !!!!!!!

¡!!!!!! ... Qué resultado mas interesante y tranquilizador  ... ¡!!!!!!

Entonces:              I = iⁱ = 0,20787958140365...

Le llamaremos "I" (IOTA, la décima letra del griego antiguo, para facilidad comunicativa)

¿No les parece fantástico que un número imaginario elevado a la potencia de un número imaginario sea un número real fácil de trabajar?

  Por otro lado: ¿No será el número  imaginario más real 
....................... y  más racional de lo parece?

Desde luego que el número imaginario formalmente no pertenece al “conjunto de los números reales” ni al “conjunto de los números racionales”, pero esto es sólo por la forma en que fueron definidos, que tiene mucho que ver por el orden histórico en que fueron estudiados.

La verdad es que el número imaginario es tan real como cualquier otro natural, entero o fraccionario, ya que se ocupa igualmente para describir la realidad, y es tan racional y entendible como cualquier número irracional ( π, e, Φ, √¯2 ).

Aunque debo confesar que no entiendo porqué unos números tan populares e importantes tienen infinita cantidad de decimales, pudiendo haber sido enteros. Como que aveces  el diseño de la naturaleza nos complica las cosas... y eso sin entrar en el tema de género.

Cuando los Pitagóricos (siglo III A.C.) se toparon con  √¯2 , dicen que hiceron un pacto de sangre para no divulgar el insólito hecho de un número que no presentaba ninguna regularidad en sus decimales y por lo tanto no podía expresarse como una fracción, y esto echaba por tierra el modelo matemático de comprensión del mundo, ... parece que al chismoso que lo divulgó por allí, lo mandaron a matar.

Un poco después, cuando ya se habían familiarizado con los “números iracionales”, en el siglo XVII, otro dolor de cabeza: el número imaginario, como lo llamó despectivamente René Descartes, esta vez no hubo muertos reconocidos, pero le dejó una mala sombra de irreal o esotérico al pobre numerito.

Hay muchas formas de verlo con naturalidad, ensayemos una:

En múltiples ocaciones se dan problemas cotidianos donde se necesitan resolver con ecuaciones como:

(1):   x²  - 1 = 0          y          (2):   x² + 1 = 0

En el primer caso tenemos que:    x²  = 1   con 2 soluciones:

(1.1):   x  =  a  = +1        y       (1.2):   x  =  u  =  -1

Con (1.1) podemos definir el “conjunto de los enteros positivos” como:

El conjunto de todos los números a·n, donde n es número natural. Análogamente se puede definir los reales positivos.

Con (1.2) podemos definir el “conjunto de los enteros negativos” como:

El conjunto de todos los números u·n, donde n es número natural. Análogamente se puede definir los reales negativos.

En el segundo caso (2), tenemos que:    x²  = -1   con la solución:

(2.1):   x  =  i  = *1        (usé el signo *, sólo porque está en el teclado).

Con (2.1) podemos definir el “conjunto de los complejos” como:

El conjunto de todos los números i·n, donde n es número real.

Análogamente se puden definir los complejos positivos, etc.

Al igual que en los números reales, también en los número complejos, están definidas perfectamente las reglas de operación y sus propiedades. Incluso se grafican en el plano cartesiano en forma análoga a como se establecen los pares ordenados para los números reales normales.

Ahora podemos ver con naturalidad:

 iⁱ  = 0,207...,        1¹ = 1,        2² = 4,          3³ = 27
    

√¯1 = ± 1,       √¯2 = ± 1,414...,     √¯3 = ± 1,732...,         √¯4 = ± 2

Así que todo es un asunto de cómo se definen los entes matemáticos y sus propiedades, y los números imaginarios son tan reales como los números reales y viceversa.

Para ampliar información básica sobre el Número Imaginario, su historia y aplicaciones matemáticas dentro del conjunto de los números complejos, ver:

http://thales.cica.es/rd/Recursos/rd98/Matematicas/09/matematicas-09.html

También es interesante la respuesta de Isaac Asimov a la pregunta:

¿Qué son los números imaginarios?, puede verla en:

https://www.ecured.cu/N%C3%BAmeros_imaginarios

INICIO
www.IBOenWEB.com