 ...
...
EL
NÚMERO CERO
El número cero ocupa un papel primordial en la
historia del desarrollo de la abstracción por parte del ser humano. Aunque se
dice que filosóficamente aparece en la cultura de
EL CERO EN
LA MATEMÁTICA MODERNA
Se simboliza como “
Valor
nulo de una magnitud.
Varios conjuntos de números incluyen al cero.
a)
En la suma, el cero es el elemento neutro, es decir, cualquier número a,
sumado con 0 vuelve a dar a. Ejemplo: 25+0=25
b)
En el producto, el cero es el elemento absorbente, cualquier número operado con 0 da
0. Ejemplo: 25x0=0
c) El 0 dividido por todo número es 0,
salvo 0. Ejemplo: 0÷8=0
Cero dividido por cero se considera
un resultado indefinido, ya que
según sea el caso, aplicando límites el resultado puede ser cualquier número.
d) División por cero: El cero es el único número real por
el cual no se puede dividir. La razón es que 0 es el único número real que no
tiene inverso multiplicativo. Matemáticamente, un número dividido por cero, tiende a infinito.
e) Cero factorial es igual a uno, 0! = 1
f) En trigonometría: (cos π/2 =
0) y (sen π = 0)
g) Logaritmo natural: ln(e) =
1, Logaritmo común: log(1) = 0
Sistemas
Digitales: el “
0”
se asocia con la posición de
"apagado" en lógica positiva y es uno de los dos dígitos del sistema
binario.
El sistema binario (0 y 1), es la base de neurotransmisores del
cerebro, así como el sistema básico de las computadoras.
... .
.
En la ciudad hindú de Gwalior, a 400 kilómetros de Nueva Delhi, se erigió a finales del siglo IX un pequeño templo dedicado al dios Visnú. Las dimensiones del jardín, como quedó recogido en una placa conmemorativa, eran de 270 hastas de largo por 187 hastas de ancho (una hasta es una unidad de medida tradicional hindú que iba desde el codo hasta la punta del dedo índice, es decir, algo menos de medio metro). Merece la pena verlo ampliado, pues se trata de la primera representación que se conoce del número cero tal y como lo escribimos hoy.
Adjunto un resumen de notas
históricas relevantes sobre el cero, tomadas principalmente de un artículo
elaborado por Manuel Herman Capitán.
El cero tuvo una larga trayectoria de comprensión e
incorporación a la cultura, primero apareció como concepto de pausa, hasta hace
pocos siglos que se instaló como cifra.
Lo primero que hay que decir sobre el cero es que hay dos usos para el cero,
ambos extremadamente importantes, pero algo distintos. Un uso es como indicador de lugar vacío en nuestro sistema
numérico de valor por posición. Así pues en un número como 2106 el cero es
usado para que las posiciones de 2 y de 1 sean correctas. Claramente 216
significa algo bastante distinto. El
segundo uso del cero es como un número mismo en la forma que lo usamos como
0. Hay también otros aspectos distintos del cero en estos dos usos, a saber, el
concepto, la notación y el nombre. (Nuestro nombre “cero” deriva del árabe sifr el cual también nos da la palabra
"cifra".)
Ninguno de los usos de arriba tiene una fácil descripción histórica. No sucedió
que alguien inventó las ideas y entonces todo el mundo comenzó a usarlos.
También es justo decir que el número
cero está lejos de ser un concepto intuitivo. Los problemas matemáticos
comenzaron como problemas “reales” más que como problemas abstractos. Los
números en los primeros momentos de la historia eran concebidos de una forma
mucho más concreta que los abstractos conceptos que son nuestros números de
hoy.
Hay un salto mental gigantesco de 5 caballos a 5
“cosas” y de ahí a la idea abstracta de “cinco”. Si los antiguos resolvían un
problema sobre cuántos caballos necesitaba un granjero el problema no iba a
tener un resultado de 0 o -23 como respuesta.
Se podría pensar que una vez que aparece un sistema numérico de valor por
posición entonces el 0 como indicador de posición vacía es una idea necesaria,
aunque los babilonios tuvieron un sistema numérico de valor por posición sin
esta característica durante 1000 años. Además no hay ninguna evidencia de que
los babilonios sintiesen que había algún problema con la ambigüedad que
existía. Extraordinariamente, sobrevivieron textos originales de la época de
los matemáticos babilonios. Los babilonios escribían en tablas de arcilla sin
cocer, usando escritura cuneiforme. Los símbolos se escribían en las tablas de
arcilla blanda con el afilado ángulo de una aguja y por esto tienen una forma
de cuña (de aquí el nombre de cuneiforme). Sobrevivieron muchas tablas
alrededor del año
Las dos cuñas no fue la única notación que usaron, de hecho, en una tabla
encontrada en Kish, una antigua ciudad de Mesopotamia situada al Este de Babilonia en lo que hoy
sería la parte centro-sur de Irak, se usó una notación distinta. Esta tabla,
que se piensa que data del
Podemos ver de esto que el primer uso del cero para denotar un espacio vacío no
es en realidad un uso del cero como número después de todo, sino meramente el
uso de algún tipo de signo de puntuación para que los números tengan una
interpretación correcta.
Los antiguos griegos comenzaron sus contribuciones a las matemáticas sobre la
época en la que el cero como indicador de posición vacía empezaba a usarse por
los matemáticos babilonios. Los griegos sin embargo no adoptaron un sistema
numérico posicional. Merece la pena pensar lo
significativo que es este hecho. ¿Cómo podían con los brillantes avances
matemáticos de los griegos no verlos adoptar un sistema numérico con las
ventajas del sistema de valor por posición que poseían los babilonios? La
verdadera respuesta a esta pregunta es más sutil que la simple respuesta que
vamos a dar, pero básicamente los logros matemáticos griegos estaban basados en
la geometría. Aunque el Elementos de Euclides contenía un libro sobre Teoría Numérica, este
estaba basado en la geometría. En otras palabras, los matemáticos griegos no necesitaban nombrar los números dado que
trabajaban con números como longitudes de una línea. Los números que
requerían ser nombrados eran usados por los mercaderes, no los matemáticos, y
de aquí que no necesitasen una notación clara.
Aunque existieron excepciones a lo que hemos afirmado. Las excepciones fueron
los matemáticos que estaban involucrados en el registro de datos astronómicos.
Aquí encontramos el primer uso del símbolo que hoy reconocemos para el cero,
los astrónomos griegos comenzaron a usar el símbolo O. Hay muchas teorías
acerca de por qué se usó este símbolo en particular. Algunos historiadores
están a favor de la explicación de que es omicrón, la primera letra de la
palabra griega para nada, es decir “ouden”. Neugebauer, sin embargo, descarta esta explicación dado que
los griegos ya usaban omicrón como un número – representaba el 70 (el sistema
numérico de los griegos estaba basado en su alfabeto).Otra explicación ofrecida
incluye el hecho de que significa “obol”, una moneda
sin casi valor, y que surge cuando se usaban fichas para contar en una tabla de
arena. La sugerencia aquí es que cuando se eliminaba una ficha para dejar una
columna vacía el hueco en la arena parecía un O.
Ptolomeo en el Almagest escrito alrededor del 130 D.C usó el sistema babilonio sexagesimal junto con el parámetro de vacío O. En esta época Ptolomeo usaba el
símbolo tanto entre dígitos como al final del número y uno estaría tentado a
creer que al menos el cero como parámetro vacío se había establecido con
firmeza. Esto, sin embargo, está lejos de lo que sucedió. Solo unos pocos
astrónomos excepcionales usaron la notación y cayeron en desuso varias veces
antes de establecerse finalmente. La idea del lugar cero (ciertamente no concebido como un número por Ptolomeo quien aún lo
consideraba un signo de puntuación) hace su siguiente aparición en los
matemáticos indios.
La escena ahora se mueve a
... el concepto matemático del cero ... estaba
presente también en la forma espiritual desde hace 17 000 años en
Lo
Alrededor del 500 D.C Aryabhata ideó un sistema numérico que no tenía aún el cero y que era un sistema posicional. Usó la palabra "kha" para la posición
y sería usado más tarde como nombre para el cero. Hay pruebas de que se había
usado el punto en los primeros manuscritos indios para denotar un espacio vacío
en la notación posicional. Es interesante que los
mismo documentos a veces también usan un punto para denotar algo desconocido
donde nosotros usaríamos x. Posteriores matemáticos indios han
nombrado el cero en números posicionales pero aún no
tenían un símbolo para el mismo. El primero registro del uso indio del cero
datado y sobre el que todos están de acuerdo en que es genuino fue escrito en
el año 876.
Tenemos una inscripción en una tabla de piedra la cual contiene una fecha que
se traduce por 876. La inscripción concierne a la ciudad de Gwalior,
Podemos considerar ahora la primera aparición del cero como número. Primero
apuntar que este no es un candidato natural para número en cierto sentido.
Desde los inicios, los números son palabras para referirnos a colecciones de
objetos. Ciertamente la idea de número se convierte en más y más abstracta y
esta abstracción hace posible la consideración del cero y de los números
negativos los cuales no habían surgido como propiedades de las colecciones de
objetos.
Por supuesto el problema que surge cuando se intenta
considerar el cero y los números negativos es cómo interactúan respecto a las
operaciones aritméticas, suma, resta, multiplicación y división. En tres
importantes libros los matemáticos indios Brahmagupta, Mahavira y Bhaskara intentaron dar respuesta a estas preguntas.
Brahmagupta intentó dar las reglas para la aritmética
teniendo en cuenta el cero y los números negativos en el siglo séptimo. Explicó
que dado un número si lo restas a sí mismo obtienes el cero. Dio las siguientes
reglas para la suma que implicaban al cero:-
La suma de cero y un número negativo, es negativo, la suma de un número positivo
y cero es positivo, la suma de cero y cero es cero.
La resta es un poco más compleja:-
Un número negativo restado de cero es positivo, un número positivo restado
de cero es negativo, cero restado de un número negativo es negativo, cero
restado de un número positivo es positivo, cero restado de cero es cero.
Brahmagupta entonces dice que cualquier número
multiplicado por cero es cero pero tiene una dificultad con la división:-
Un número positivo o negativo cuando es dividido por cero es una fracción
con cero como denominador. Cero dividido por un número positivo o negativo es o
cero o expresado como fracción el cero como numerador y una cantidad finita
como denominador. Cero dividido por cero es cero.
En verdad Brahmagupta está diciendo muy poco cuando
sugiere que n dividido por 0 es n/0. Claramente
tiene un problema con esto. Ciertamente está equivocado cuando afirma que cero
dividido por cero es cero. Sin embargo es un intento brillante por parte de la
primera persona que sabemos que intentó extender la aritmética a los números
negativos y el cero.
En 830, alrededor de 200 años después de que Brahmagupta escribiese su obra maestra, Mahavira escribió Ganita
Sara Samgraha que fue diseñado como una actualización
del libro de Brahmagupta. Afirma correctamente que:-
... un número multiplicado por cero es cero, y un número permanece igual si
se le resta cero.
Sin embargo sus intentos de mejorar las afirmaciones de Brahmagupta sobre la división por cero parecen llevarle al error. Escribe:-
Un número permanece sin cambio cuando es dividido por cero.
Por tanto, Bhaskara intentó resolver el problema
escribiendo que n/0 = ∞.
A primera vista podríamos estar tentados a pensar que Bhaskara estaba en lo cierto, pero por supuesto no lo
estaba. Si fuese cierto entonces 0 veces ∞ debe ser igual a cada número
n, por tanto todos los número son iguales. Los matemáticos indios no podían
llegar al punto de admitir que no se puede dividir por cero. Bhaskara hizo otra afirmación correcta sobre las
propiedades del cero, no obstante, como que 02 = 0 y que √0 =
0.
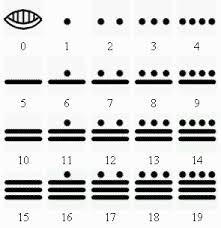
Es importante hacer notar en este punto que hubo otra civilización que desarrolló un sistema numérico de valor por
posición con el cero. Fueron los Mayas, que vivieron
en Centro América. Esta fue una antigua civilización que floreció
particularmente entre el 250 y 900. Sabemos que sobre el 665 usaron un sistema
numérico de valor por posición de base 20 con un símbolo para el cero. Sin
embargo, su uso del cero iba más allá de esto y estaba en uso antes de que lo
introdujesen en el sistema numérico de valor por posición. Esto es un notable
éxito pero desgraciadamente no influenció a otras culturas.
El brillante trabajo de los matemáticos indios fue transmitido a los
matemáticos árabes e islámicos del lejano occidente. Llegó una primera etapa
donde al-Khwarizmi escribió Al'Khwarizmi en el arte Hindú del Cálculo en cual describe el sistema numérico indio de
valor por posición de cifras basado en 1, 2, 3, 4, 5, 6, 7, 8, 9, y 0. Este
trabajo fue el primero en lo que ahora es Irak en usar el cero como marcador de
posición en una notación de base posicional.
Ibn Ezra, en el siglo XII, escribió tres tratados sobre números que ayudaron a traer los
símbolos e ideas indias de las fracciones decimales a la atención de algunos de
los estudiantes europeos. El Libro de los Números describe el sistema
decimal para enteros con valores de posición de izquierda a derecha. En este
trabajo Ibn Ezra usa el cero,
al que llama galgal (significa rueda o círculo).
Ligeramente más tarde en el siglo XII al-Samawal escribió:-
Si restamos un número positivo de cero permanece el mismo número negativo...
si restamos un número negativo de cero nos queda el mismo número positivo.
Las ideas se dispersaron hacia el Este, a China, así como al Oeste a los países
islámicos. En 1247 el matemático chino Ch'in Chiu-Shao escribió Tratado
matemático en nueve secciones en el cual usa el símbolo O para el cero. Un
poco más tarde, en 1303, Zhu Shijie escribió El espejo de Jade de los cuatro elementos en el cual usa de
nuevo el símbolo O para el cero.
Fibonacci fue una de las principales personas en
traer estas nuevas ideas sobre sistemas numéricos a Europa. Se considera
que: un importante nexo entre el sistema numérico Arábico-Hindú y el los matemáticos
europeos es el matemático italiano Fibonacci.
En Liber Abaci describe los
nueve símbolos indios junto con el signo 0 para los europeos alrededor del año
1200 pero no fue usado ampliamente hasta bastante tiempo después. Es
significativo que Fibonacci no fue lo bastante audaz
como para tratar el 0 de la misma forma que al resto de números 1, 2, 3, 4, 5,
6, 7, 8, 9 dado que habla de la “marca” cero mientras que al resto de símbolos
los llama números. Aunque traer los números indios a Europa fue claramente de
una gran importancia podemos ver en su tratamiento del cero que no alcanzó la
misma sofisticación que los indios Brahmagupta, Mahavira y Bhaskara ni la de los
matemáticos árabes e islámicos como al-Samawal.
Por supuesto aún hay signos de los problemas causados por el cero.
Recientemente mucha gente de todo el mundo celebró el nuevo milenio en 1 de
Enero de 2000. Por supuesto celebraron el paso de solo 1999 años dado que el
calendario no tienen ningún año cero especificado.
Aunque se podría olvidar el error original, es un tanto sorprendente que la
mayoría de gente sea incapaz de comprender por qué el tercer milenio y el siglo
XXI comenzaron el 1 de Enero de 2001. ¡El cero continúa causando problemas!
 .
.
A continuación se presenta un resumen de
consideraciones sobre el cero y el concepto de número, extraído principalmente
de notas de Abelardo Falletti.
Número,
en matemáticas, es un símbolo utilizado para designar cantidades o
entidades que se comporten como tales.
Y
a su vez matemáticas significa el estudio de las relaciones entre cantidades,
magnitudes y propiedades, como así también de las operaciones lógicas
utilizadas para deducir cantidades, magnitudes y propiedades desconocidas.
Hacia
mediados del siglo XIX las matemáticas se empezaron a considerar como la ciencia
de las relaciones, o como la ciencia que produce condiciones necesarias.
Los
números naturales son:
1,
2, 3, 4, 5, 6, 7, 8 y 9
Estos
números naturales son los primeros números que surgen sin diferencia alguna en
las distintas civilizaciones. Es una cosa muy sugestiva porque podría estar
indicando que se trata de una estructura genética en el hombre, mientras que
los números posteriores al 9 aparecen como sistemas convencionales de lo más
diversos hasta concluir con la adopción del sistema decimal.
Sin
embargo en la actualidad dichos números naturales suelen iniciarse matemáticamente con "Cero", y continúa la serie más allá del 9 de un
modo relativamente infinito a partir del 10.
Se
trata de una convención dentro de la especialidad científica de las matemáticas
para facilitar el sistema de contar y permitir su notación posicional.
Por
lo tanto el cero no es un número porque por sí mismo no designa cantidades,
sino que permite convencionalmente que los números combinados con el cero
puedan facilitar los cálculos que designan cantidades mayores a 9.
De
lo contrario, los dedos de la mano tendrían que comenzar a contarse desde el
"cero" y la suma de los dedos de una mano daría "cuatro".
Obviamente se trata de una contradicción en relación con la natural forma de
contar que tiene el ser humano.
El
símbolo del cero permite aumentar o disminuir el valor del círculo numérico 1
al 9, y mezclado con ellos los posiciona de un modo tal que perfecciona el
sistema de cálculos.
Se
trata de una convención planetaria unívoca, y por lo tanto las relaciones a que
se refiere la definición de las matemáticas son posibles de descodificar en
cualquier rincón del planeta, y por cualquier persona humana, con el mismo
significado. Este es un logro que no han alcanzado las otras disciplinas
científicas cuyas convenciones para establecer un lenguaje unívoco sólo se
aplican dentro de cada especialidad.
En
la edad media existían seis grupos culturales bien diferenciados, que pueden
clasificarse como Occidente latino, Oriente bizantino, China, India, la
civilización musulmana, y la civilización Maya.
Fueron
los mayas quienes descubrieron la utilidad de incorporar un símbolo llamado
"cero" para perfeccionar el sistema de contar que necesitaban para sus
cálculos astronómicos.
Esta
incorporación de la civilización Maya derivó en el sistema corriente de
notación numérica que es utilizado actualmente en casi todo el mundo sobre la
base de la numeración arábiga. La innovación aportada por el sistema arábigo
fue el uso de la notación posicional, mediante la
cual los nueve símbolos numéricos cambian su valor según la posición que ocupen
en la cifra escrita.
Esta
notación posicional no es posible sin la presencia de
un símbolo, no numérico y a este solo efecto, denominado "cero", se
le otorgue el símbolo y el nombre que se quiera.
Ese
símbolo "cero", por sí mismo, permite distinguir entre 35, 305, 3500,
3005, por ejemplo, sin necesidad de utilizar símbolos adicionales,
simplificando de tal modo cualquier tipo de cálculo numérico por escrito o
notación. Y el hábito hizo lo demás, porque se han establecido relaciones
habituales entre las diferentes notaciones que permiten darle a cada una de
ellas el significado correspondiente.
Es algo similar a lo que ocurre con
las notaciones musicales para los músicos, con la salvedad de que estas notaciones no son
conocidas ni habituales por todos los habitantes del planeta durante centurias
como ha ocurrido y ocurre con el sistema decimal y sus notaciones, además de
ser colectivamente instruidos convenientemente en la educación primaria sobre
las bases del sistema.
El "cero" no sólo
significa vacío,
ausencia de número, sino que si se imagina a un nadador que salta desde un bote
inmóvil flotando en el agua puede encontrarse ese mismo significado. Antes de
saltar el nadador y el bote carecen de movimiento, motivo por el cual el
momento lineal es "cero", es decir nulo. Al saltar, el nadador
adquiere momento lineal hacia adelante de él y al mismo tiempo el bote se mueve
hacia atrás con un momento igual en magnitud y dirección pero en sentido
contrario. Esto significa que el momento total del sistema formado por el
nadador y el bote sigue siendo "cero", es decir ausencia de momento lineal.
La conservación del momento lineal
se cumple en la teoría cuántica, al describir los fenómenos atómicos y nucleares, como así
también en la relatividad cuando los sistemas se desplazan a velocidades
próximas a la de la luz.
El concepto de cero absoluto también es importante desde el punto de vista teórico. Según la tercera ley de
la termodinámica, la entropía de un cristal puro sería nula en el cero
absoluto. Esto tiene una destacada importancia en las reacciones químicas y en
la física cuántica, porque los materiales tienen propiedades muy extrañas
cuando se enfrían a temperaturas muy bajas. Por ejemplo, algunos pierden por
completo su resistencia eléctrica, tal como se pudo observar en el mercurio a
unos pocos grados por encima del concepto del cero absoluto.
En
teoría, las moléculas de una sustancia no presentan actividad traslacional alguna a la temperatura conceptual de cero absoluto.
En
el sistema binario que utilizan los ordenadores con el sistema de interruptores
la posición de encendido corresponde convencionalmente al uno, y el
"apagado" al cero. También se pueden usar puntos imantados en una
cinta magnética o disco, en el que un punto imantado representa al dígito 1, y
la ausencia de un punto imantado es el dígito "cero".
Es
decir, el "cero" implica siempre "ausencia". Y
matemáticamente significa "vacío de cantidad", "ausencia de
número", siendo al mismo tiempo un "cero absoluto" porque en sí
mismo no es positivo ni negativo.
Tan
sólo conceptualmente se lo puede llegar a considerar como "cero
negativo" y "cero positivo", dependiendo ello de la dirección
operativa con la cual se llega al cero, según estos ejemplos:
+
15 - 9 - 6 = + 0
-
15 + 9 + 6 = - 0
Se
trata de un concepto, porque el cero entrará en la operatoria matemática sin
cambio alguno se trate de una dirección de llegada al mismo en sentido positivo
o negativo.
El Cero está definido en matemáticas
como el representante de un conjunto vacío cuyo símbolo es el cero.

LEONARDO Y
http://webs.adam.es/rllorens/picuad/leonardo.htm
